剑指Offer JavaScript-递归循环专题

青蛙跳台阶

1. 题目描述

一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

2. 思路分析

跳到 n 阶假设有 f(n)种方法。

往前倒退，如果青蛙最后一次是跳了 2 阶，那么之前有 f(n-2)种跳法; 如果最后一次跳了 1 阶，那么之前有 f(n-1)种跳法。

所以：f(n) = f(n-1) + f(n-2)。就是斐波那契数列。

3. 代码

这里利用缓存模式（又称备忘录模式）实现了代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
const fibonacci = (() => {
    let mem = new Map();
    mem.set(1, 1);
    mem.set(2, 1);

    const _fibonacci = (n) => {
        if (n <= 0) {
            throw new Error("Unvalid param");
        }

        if (mem.has(n)) {
            return mem.get(n);
        }

        mem.set(n, _fibonacci(n - 1) + _fibonacci(n - 2));
        return mem.get(n);
    };

    return _fibonacci;
})();

/**
 * 测试代码
 */

let start = new Date().getTime(),
    end = null;

fibonacci(8000);
end = new Date().getTime();
console.log(`耗时为${end - start}ms`);

start = end;
fibonacci(8000);
end = new Date().getTime();
console.log(`耗时为${end - start}ms`);

数值的整次方

1. 题目描述

题目：实现函数 double Power（double base, intexponent），求 base 的 exponent 次方。不得使用库函数，同时不需要考虑大数问题

2. 思路分析

简单思路：最简单的做法是循环，但是要考虑异常值的检验。比如指数是负数，底数为 0。

优化思路：书上提供了一种复杂度为 $O(logN)$ 的做法。比如我们要求 32 次方，那么只要求出 16 次方再平方即可。依次类推，是递归函数的结构。

递推公式如下：

$$
a^n=\left{
\begin{aligned}
a^{n/2}*a^{n/2} ; n为偶数\
a^{(n - 1)/2}*a^{(n - 1)/2} ; n为奇数
\end{aligned}
\right.
$$

需要注意的是，如果幂是奇数，例如 5 次方，可以先计算 2 次方，结果平方后（4 次方），再乘以自身（5 次方）。按照此思路处理。

代码实现-简单思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 *
 * @param {Number} base
 * @param {Number} exp
 */
function pow(base, exp) {
    // 规定0的任何次方均为0
    if (!base) {
        return 0;
    }
    let result = 1,
        absExp = Math.abs(exp);

    for (let i = 0; i < absExp; ++i) {
        result *= base;
    }

    // 对于指数小于0的情况，求其倒数
    if (exp < 0) {
        result = 1 / result;
    }

    return result;
}

/**
 * 以下是测试代码
 */

console.log(pow(2, -2));
console.log(pow(2, 2));
console.log(pow(2, 0));
console.log(pow(0, -9));

代码实现-优化思路

在 Js 中整数除 2 不会自动取整，可以使用Math.floor()。但更好的做法是使用>>位运算。

判断奇数可以用%2判断。但更好的做法是和1进行&运算后（除了最后 1 位，都被置 0 了），判断是不是 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * 求base 的 exp次幂，其中exp永远是正数
 * @param {Number} base
 * @param {Number} exp
 */
function unsignedPow(base, exp) {
    if (exp === 0) {
        return 1;
    } else if (exp === 1) {
        return base;
    }

    let result = pow(base, exp >> 1);
    result *= result;
    if (exp & (1 === 1)) {
        result *= base;
    }

    return result;
}

/**
 * 求 base的exp次幂
 * @param {Number} base
 * @param {Number} exp
 */
function pow(base, exp) {
    if (!base) {
        return 0;
    }

    let absExp = Math.abs(exp);

    return exp < 0 ? 1 / unsignedPow(base, absExp) : unsignedPow(base, absExp);
}

/**
 * 以下是测试代码
 */

console.log(pow(2, 2));
console.log(pow(2, 0));
console.log(pow(0, -9));
console.log(pow(2, -2));

打印从1到最大的n位数

1. 题目描述

题目：输入数字 n，按顺序打印出从 1 最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数即 999。

2. 思路分析

主要的坑点在：大数的溢出。当然，es6 提供了BigInt数据类型，可以直接相加不用担心溢出。

除此之外，这题显然是要我们模拟“大数相加”：将最低位加 1，然后每次检查是否进位，如果不进位，直接退出循环；如果进位，需要保留进上来的 1，然后加到下一位，直到不进位或者超出了我们规定的范围。

3. 代码实现

js 中不方便操作字符串中指定位置的字符，因此用数组对象来模拟。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
/**
 * 用数组模拟大数相加操作
 * @param {Array} arr
 * @return {Boolean} true, 超出arr.length位最大整数; false, 没有超出arr.length位最大整数
 */
function increase(arr) {
    let length = arr.length,
        over = 0; // 记录前一位相加后的进位数

    for (let i = length - 1; i >= 0; --i) {
        arr[i] = arr[i] + over;

        if (i === length - 1) {
            arr[i] += 1;
        }

        if (arr[i] >= 10) {
            // 如果第n位进位，说明超出了n位最大数字
            if (i === 0) {
                return true;
            }

            arr[i] = arr[i] - 10;
            over = 1;
        } else {
            break;
        }
    }

    return false;
}

/**
 *
 * @param {Number} n
 */
function printMaxDigits(n) {
    if (n <= 0) {
        return;
    }

    let arr = new Array(n).fill(0);
    while (!increase(arr)) {
        console.log(arr);
    }
}

/**
 * 测试代码
 */
printMaxDigits(2);
printMaxDigits(3);
printMaxDigits(10);

顺时针打印矩阵

1. 题目描述

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

2. 思路分析

既然是顺时针打印，其实就是由外向内一圈圈打印，将过程分为 2 步：

第一步：printMatrix函数，确定要打印的圈的左上角坐标（比较简单）

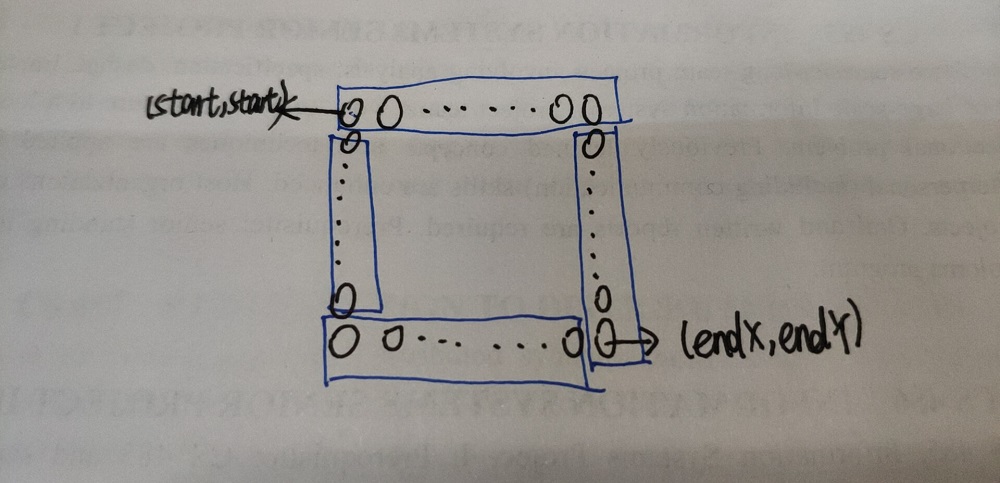
第二步：printMatrixInCircle函数，根据左上角坐标，顺时针打印这一圈的信息。这个过程又分为四步：左上 -> 右上 -> 右下 -> 左下 -> 左上。

3. 代码实现

如果觉得，函数printMatrixInCircle的条件判断不清楚，可以配合下面这张图一起看：

5cfcfe24760b637950.jpg

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
/**
 * 打印从 (start, start) 与 (endX, endY) 围成的一圈矩形
 * @param {Array} arr
 * @param {Number} cols
 * @param {Number} rows
 * @param {Number} start
 */
function printMatrixInCircle(arr, cols, rows, start) {
    let endX = cols - start - 1,
        endY = rows - start - 1,
        result = "";

    // 从 左上 到 右上 打印一行
    for (let i = start; i <= endX; ++i) {
        result = result + " " + arr[start][i];
    }

    // 从 右上 到 右下 打印一行
    if (start < endY) {
        for (let i = start + 1; i <= endY; ++i) {
            result = result + " " + arr[i][endX];
        }
    }

    // 从 右下 到 左下 打印一行
    if (start < endX && start < endY) {
        for (let i = endX - 1; i >= start; --i) {
            result = result + " " + arr[endY][i];
        }
    }

    // 从 左下 到 左上 打印一行
    if (start < endX && start < endY - 1) {
        for (let i = endY - 1; i >= start + 1; --i) {
            result = result + " " + arr[i][start];
        }
    }

    console.log(result);
}

/**
 * 打印的外层函数, 主要用于控制要打印的圈
 * @param {Array} arr
 */
function printMatrix(arr) {
    if (!Array.isArray(arr) || !Array.isArray(arr[0])) {
        return;
    }

    let start = 0,
        cols = arr[0].length,
        rows = arr.length;

    while (cols > start * 2 && rows > start * 2) {
        console.log(`第${start + 1}层: `);
        printMatrixInCircle(arr, cols, rows, start);
        ++start;
    }
}

/**
 * 以下是测试代码
 */

printMatrix([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9],
]);

printMatrix([
    [1, 2, 3, 4],
    [4, 5, 6, 7],
    [8, 9, 10, 11],
]);

数组中出现次数超过一半的数字

1. 题目描述

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为 9 的数组{1,2,3,2,2,2,5,4,2}。

由于数字 2 在数组中出现了 5 次，超过数组长度的一半，因此输出 2。

2. 思路分析

数组中有一个数字出现的次数超过数组长度的一半，说明它出现的次数比其他所有数字出现次数的和还要多。

在遍历的过程中保存两个变量：一个数字 + 一个次数。遍历到每个元素都会更新次数，元素 = 数字，加次数；否则，减次数；如果次数为 0，当前元素赋值给数字。

需要注意的是，最后结果不一定符合条件，比如数组 [1, 2, 3]，结果是 3。所以要再统计一下最后数字的次数，是否有一半那么多。

3. 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 检查指定元素的次数是否大于等于长度一半
function checkMoreThanHalf(nums = [], target) {
    let times = 0;
    nums.forEach((num) => num === target && ++times);
    return times * 2 >= nums.length;
}

// 计算出数组元素
function moreThanHalfNum(nums = []) {
    if (!Array.isArray(nums) || !nums.length) {
        return null;
    }

    let times = 1,
        result = nums[0];
    for (let i = 1; i < nums.length; ++i) {
        if (times === 0) {
            times = 1;
            result = nums[i];
        } else if (result === nums[i]) {
            ++times;
        } else {
            --times;
        }
    }

    return checkMoreThanHalf(nums, result) ? result : null;
}

/**
 * 以下是测试代码
 */

console.log(moreThanHalfNum([3, 1, 3, 2, 2])); // output: null
console.log(moreThanHalfNum([1, 2, 3, 2, 2, 2, 5, 4, 2])); // output: 2

最小的k个数

1. 题目描述

输入 n 个整数，找出其中最小的 k 个数。例如输入 4、5、1、6、2、7、3、8 这 8 个数字，则最小的 4 个数字是 1、2、3、4。

2. 思路分析

利用“快速排序”的中的 partition 操作：返回 index，小于 index 对应元素的元素都放在了左边，大于 index 对应元素的元素都放在右边。

利用这个特性，只要我们的 partition 返回值是 k - 1，那么数组中前 k 个元素已经被摆放到了正确位置，直接遍历输出即可。

由于不需要排序全部，整体的时间复杂度是 O(N)。但美中不足的是：要在原数组操作，除非用 O(N)的空间来做拷贝。除此之外，针对海量动态增加的数据，也不能很好处理。这种情况需要用到“最大堆”，请前往《堆》章节查看。

3. 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
function partiton(arr = [], start, end) {
    const length = arr.length;
    if (!length) {
        return null;
    }

    let v = arr[start],
        left = start + 1,
        right = end;

    while (1) {
        while (left <= end && arr[left] <= v) ++left;
        while (right >= start + 1 && arr[right] >= v) --right;

        if (left >= right) {
            break;
        }

        [arr[left], arr[right]] = [arr[right], arr[left]];
        ++left;
        --right;
    }

    [arr[right], arr[start]] = [arr[start], arr[right]];
    return right;
}

function getKthNumbers(nums = [], k) {
    if (k <= 0) {
        return null;
    }

    const length = nums.length;
    const result = new Array(k);
    let start = 0,
        end = length - 1;
    let index = partiton(nums, start, end);
    while (index !== k - 1) {
        if (index > k - 1) {
            // 前k个元素在 [start, index] 下标范围内
            // 要进一步处理，缩小区间
            end = index - 1;
            index = partiton(nums, start, end);
        } else {
            // [start, index]都属于小于k的元素，但不是全部
            // 剩下要处理的区间是 [index + 1, end]
            start = index + 1;
            index = partiton(nums, start, end);
        }
    }

    for (let i = 0; i < k; ++i) {
        result[i] = nums[i];
    }

    return result;
}

/**
 * 以下是测试代码
 */

console.log(getKthNumbers([4, 5, 1, 6, 2, 7, 3, 8], 4)); // output: [2, 3, 1, 4]
console.log(getKthNumbers([10, 2], 1));

和为s的两个数字

1. 题目描述

输入一个递增排序的数组和一个数字 s，在数组中查找两个数，使得它们的和正好是 s。如果有多对数字的和等于 s，输出任意一对即可。

2. 解题思路

如果这个数组不是递增的，就得用哈希表来解决，空间复杂度是 O(N)。

但是题目条件是“递增数组”，因此可以使用“双指针”的思路来实现：即一个指针指向开头，另一个指向结尾。

比较指针对应的 2 个元素的和与给定数组 s：

  • 元素和 > s: 后指针向前移动
  • 元素和 < s: 前指针向后移动
  • 元素和 = s: 返回指针对应的 2 个元素

3. 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 *
 * @param {Array} data
 * @param {Number} sum
 */
function findNumsWithSum(data, sum) {
    if (!Array.isArray(data) || data.length <= 1) {
        return [null, null];
    }
    let i = 0,
        j = data.length - 1;
    while (i < j) {
        let now = data[i] + data[j];
        if (now === sum) {
            return [data[i], data[j]];
        } else if (now > sum) {
            --j;
        } else {
            ++i;
        }
    }

    return [null, null];
}

/**
 * 以下是测试代码
 */

// 输出：[ 4, 11 ]
console.log(findNumsWithSum([1, 2, 4, 7, 11, 15], 15));

和为s的连续正数序列

1. 题目描述

输入一个正数 s，打印出所有和为 s 的连续正数序列（至少含有两个数）。例如输入 15，由于 1 ＋ 2 ＋ 3 ＋ 4 ＋ 5 ＝ 4 ＋ 5 ＋ 6 ＝ 7 ＋ 8 ＝ 15，所以结果打印出 3 个连续序列 1 ～ 5、4 ～ 6 和 7 ～ 8。

2. 思路分析

和前面题目很相似，这里也是“双指针”的思路。不同的地方有 2 个点：

  • 指针是从第 0 个和第 1 个位置开始的（下面称为 a 和 b）
  • 这里要计算指针范围内的所有元素和（题目要求是“连续序列”）

每次移动 a、b 之前，都要计算一下当前[a,b]范围内的所有元素和。如果等于 s，打印并且 b 右移；如果小于 s，b 右移；如果大于 s，a 右移。

至于为什么相等的时候 b 右移而不是 a 右移？因为 a 右移会漏掉情况，而且指针可能重叠。比如对于数组 [1, 2, 2]，给定 s 是 3。

3. 算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * 打印指定数组的起始下标内的所有元素
 *
 * @param {Array} data 打印数组
 * @param {Array} seq [start, end] 数组打印元素的起始下标
 */
function print(data, seq) {
    const [start, end] = seq;
    for (let i = start; i <= end; ++i) {
        process.stdout.write(data[i] + ", ");
    }
    process.stdout.write("\\n");
}

/**
 * 打印出递增数组中，所有和为s的元素
 *
 * @param {Array} data 递增数组
 * @param {Number} sum 和
 */
function findSequenceWithSum(data, sum) {
    let small = 0,
        big = 1,
        cur = data[small] + data[big];
    const middle = (data.length + 1) >> 1;
    while (small < middle) {
        if (cur <= sum) {
            cur === sum && print(data, [small, big]);
            ++big;
            cur += data[big];
        } else {
            cur -= data[small];
            ++small;
        }
    }
}

/**
 * 测试代码
 */

// 输出：
// 2, 3, 4,
// 4, 5,
findSequenceWithSum([1, 2, 3, 4, 5, 6, 7, 8], 9);

n个骰子的点数

1. 题目描述

把 n 个骰子扔在地上，所有骰子朝上一面的点数之和为 s。输入 n，打印出 s 的所有可能的值出现的概率。

2. 思路分析

递归的思路就是组合出所有情况，然后每种情况记录出现次数，最后除以 6^n 即可。其中，6^n 就是所有情况的总数。

书中提出的方法是使用循环来优化递归，递归是自顶向下，循环是自底向上，思考起来有难度。

技巧性很强，准备 2 个数组，假想每次投掷一个骰子，出现和为 n 的次数，就是之前骰子和为 n-1, n-2, …, n-6 的次数和。依次类推，每次存储结果都和之前的数组不同。

3. 算法实现

注释中都有详细说明：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
const gMaxValue = 6; // 每个骰子的最大点数

/**
 *
 * @param {Number} number 骰子的个数
 */
function printProbability(number) {
    if (number < 1) {
        return;
    }

    const probabilities = [
        new Array(gMaxValue * number + 1),
        new Array(gMaxValue * number + 1),
    ];
    let flag = 0;

    // 初始化
    for (let i = 0; i < gMaxValue * number + 1; ++i) {
        probabilities[0][i] = probabilities[1][i] = 0;
    }

    // 第一次掷骰子，出现的和只有有 gMaxValue 种情况，每种和的次数为 1
    for (let i = 1; i <= gMaxValue; ++i) {
        probabilities[flag][i] = 1;
    }

    // 之后是从第 2 ~ number 次掷骰子
    //
    for (let k = 2; k <= number; ++k) {
        // 第k次掷骰子，那么最小值就是k
        // 不可能出现比k小的情况
        for (let i = 0; i < k; ++i) {
            probabilities[1 - flag][i] = 0;
        }

        // 可能出现的和的范围就是 [k, gMaxValue * k + 1)
        // 此时和为i的出现次数，就是上次循环中骰子点数和为
        // i - 1, i - 2, ..., i - 6 的次数总和
        for (let i = k; i < gMaxValue * k + 1; ++i) {
            probabilities[1 - flag][i] = 0;
            // 这里的j是指：本骰子掷出的结果
            for (let j = 1; j < i && j <= gMaxValue; ++j) {
                probabilities[1 - flag][i] += probabilities[flag][i - j];
            }
        }

        flag = 1 - flag;
    }

    // 全部情况的总数
    const total = Math.pow(gMaxValue, number);
    for (let i = number; i < gMaxValue * number + 1; ++i) {
        console.log(`sum is ${i}, ratio is ${probabilities[flag][i] / total}`);
    }
}

/**
 * 测试代码
 * 6个骰子，所有和出现的可能性
 */
printProbability(6);

扑克牌的顺子

1. 题目描述

从扑克牌中随机抽 5 张牌，判断是不是一个顺子，即这 5 张牌是不是连续的。

2 ～ 10 为数字本身，A 为 1，J 为 11，Q 为 12，K 为 13，而大、小王可以看成任意数字。

2. 思路分析

难度不大，可以将大小王看成数字 0，可以在任何不连续的两个数字之间做填充。

首先将原数组排序，然后统计任意数字（0）的出现次数。再遍历之后的数字，找出不相邻数字之间总共差多少个数字。

最后比较 0 的出现次数和总共差多少个数字，两者的大小关系。

注意：连续两个相同的数字是对子，不符合要求。

3. 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 *
 * @param {Array} numbers
 */
function isContinuous(numbers) {
    numbers.sort();
    const length = numbers.length;

    let zeroNum = 0;
    for (let i = 0; i < length && !numbers[i]; ++i) {
        ++zeroNum;
    }

    let interval = 0;
    for (let i = zeroNum + 1; i < length - 1; ++i) {
        if (numbers[i] === numbers[i + 1]) {
            return false;
        }
        interval += numbers[i + 1] - numbers[i] - 1;
    }

    return interval <= zeroNum;
}

/**
 * 测试代码
 */
console.log(isContinuous([3, 8, 0, 0, 1])); // false
console.log(isContinuous([8, 10, 0, 6, 0])); // true

圆圈中最后剩下的数字

1. 题目

0,1,…,n-1 这 n 个数字排成一个圆圈，从数字 0 开始每次从这个圆圈里删除第 m 个数字。求出这个圆圈里剩下的最后一个数字。

2. 思路分析

这个其实是经典的“约瑟夫环”问题。常用解法就是“循环取余”。每次都把下标移动 m 个位置，然后移除当前元素。直到只剩最后一个元素。

3. 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * @param {Number} n 0, 1, 2, ..., n-1 一共n个数字
 * @param {Number} m 被删除的第m个数字(从0计算)
 */
function lastRemain(n, m) {
    // 生成 [0, 1, ... , n-1] 的列表
    const nums = new Array(n);
    for (let i = 0; i < n; ++i) {
        nums[i] = i;
    }

    // 逐步移除第m个数字
    let start = 0;
    while (nums.length > 1) {
        start = (start + m) % nums.length;
        nums.splice(start, 1);
    }

    return nums.shift();
}

/**
 * 测试函数
 */
console.log(lastRemain(5, 2));