函数式编程递归优化专题-TOC和Trampolines

递归

递归是FP中重要组成部分。递归的重点：

  • 基本条件，满足基本条件，递回停止，也可说是终止条件。
  • 若未满足，呼叫自己。
  • 每一次都逐渐往基本条件的方向收敛。

递归相较于迭代来说，代码更精简。递归是用代码去描述what，而迭代是用代码去描述how。例如对于斐波那契数列，两种写法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 递归解法
function fib(n) {
    if (n <= 1) return n;
    return fib( n - 2 ) + fib( n - 1 );
}

// 迭代解法
function fib (n) {
    var r = 0, q = 1, p;

    if (n <= 1) {
        return n
    } else {
        for (let i = 2; i <= n; i++) {
            p = r + q
            r = q
            q = p
        }
        return p
    }
}

从JS引擎优化

递归调用可以不在本次宏任务中执行，而是放在下次宏任务/微任务中运行。可以考虑使用setTimeout或者Nodejs的nextTick

如何通过WebWorker与时间分片优化JS长任务？ 也有参考意义，但是在generator函数中使用递归的效果还有待实验验证！

Tail Calls Optimizations(尾递归调用优化)

为什么会出现「爆栈」？

当递归层度增加，就可能会遇到「爆栈」的情况。为什么会出现「爆栈」的情况呢？

我们知道，函数调用会在内存形成一个”调用记录”，又称”调用帧”（call frame），保存调用位置和内部变量等信息。如果在函数A的内部调用函数B，那么在A的调用记录上方，还会形成一个B的调用记录。等到B运行结束，将结果返回到A，B的调用记录才会消失。如果函数B内部还调用函数C，那就还有一个C的调用记录栈，以此类推。所有的调用记录，就形成一个“调用栈”（call stack）。

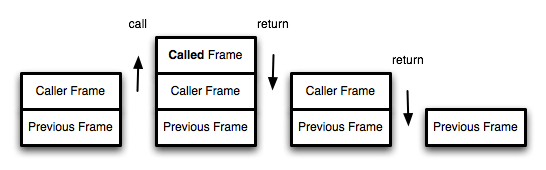
Untitled.png

当递归函数一直自我调用或者相互调用时，由于要保存回来的信息（调用帧），所以调用栈越来越大，当超过语言引擎的限制，就会抛出错误。

TCO实现流程

这时就需要使用尾递归进行优化，又简称TCO。尾递归调用是指函数最后返回的是函数的调用。这样就不需要保存调用位置、内部信息等调用帧。

对于阶乘函数来说，一个错误的TCO是：

1
2
3
4
5
6
7
function factorial (n) {
    if (n === 0) {
        return 1
    }
    return n * factorial(n - 1)
}
// 错误原因：返回的有 n* ，那么就得用调用帧去记录这个信息，方便函数返回后，计算结果，因此无法进行tco

对于阶乘函数来说，一个正确的TCO是：

1
2
3
4
5
6
7
8
9
10
"use strict"; // es6 严格模式下才有尾递归调用优化
function factorial(n, partialFactorial = 1) {
  // partialFactorial含义：之前乘积的值
  if (n === 0) {
      return partialFactorial
  }
  return factorial(n - 1, n * partialFactorial);
}
// 正确原因：只保留了一个调用记录，复杂度是O(1)。
// 底层引擎在解析+运行代码时，发现这里没有前面错误写法的 n* ，那么就不需要特殊保存调用帧。

Trampolines

TCO，为什么会称作优化呢？因为我当前的递回执行结束后，就不需要再回来，所以可以将stack frame移走，避免堆叠更多stack frame。

那如果引擎不支援TCO呢？有另外一种技巧叫做Trampolines，适合在没有TCO的环境使用。就是将递归转换为迭代。

Trampoline 是一个函数，具体是这样工作的：

  • 接受一个函数fn 当参数
  • call fn
  • 如果返回值是函数，就再call 得到返回值
  • 如果返回值不是函数，就直接返回

在这篇文章中，讲到了一个特别好的例子。可以根据这个例子，将一些符合TCO要求的递归函数，改写成迭代形式。

实现流程

step1:封装trampoline函数

1
2
3
4
5
6
7
8
9
10
function trampoline(fn) {
    return function trampolined(...args){
        var result = fn( ...args )
        // 檢查返回結果的類型，當返回一個函數時，loop 繼續
        while (typeof result === "function") {
            result = result()
        }
        return result
    }
}

step1:改写他们，让他们不再返回值，而是返回一个lazy模式的函数

1
2
3
4
5
6
7
8
9
10
11
12
13
function toSteven(n) {
  if (n === 0)
    return 'boom!'
  else
    return () => toJob(Math.abs(n) - 1);
}

function toJob(n) {
  if (n === 0)
    return undefined
  else
    return () => toSteven(Math.abs(n) - 1);
}

两个没有经过TCO优化的互相递归调用函数（参数太大会爆栈）：

1
2
3
4
5
6
7
8
9
10
11
12
13
function toSteven(n) {
  if (n === 0)
    return 'boom!'
  else
    return toJob(Math.abs(n) - 1);
}

function toJob(n) {
  if (n === 0)
    return undefined
  else
    return toSteven(Math.abs(n) - 1);
}

step3: 配合trampoline

1
2
var trampolined_toSteven = trampoline(toSteven)
var trampolined_toJob = trampoline(toJob)

step4: 见证效果

1
2
console.log(trampolined_toSteven(200000))// "boom!"
console.log(trampolined_toJob(3333333))// "boom!"

再举一个计算阶乘的例子：

1
2
3
4
5
6
function factorial(n, partialFactorial = 1) {
  if (n === 0) {
      return partialFactorial
  }
  return () => factorial(n - 1, n * partialFactorial);
}

参考

bookmark

bookmark

bookmark