最短路径问题求解以及近似最短路径

dijkstra应用场景

深度优先和广度优先，主要针对无权图的搜索。

针对有向有权图，也就是图中的每条边都有一个权重，使用的是dijkstra算法。

dijkstra建模

点（GraphNode）

注意dist属性，它是距离开始节点的最短路径距离。

1
2
3
4
5
6
7
class GraphNode {
    constructor(key) {
        this.key = key; // 节点的标识
        this.edges = []; // 节点的边
        this.dist = 0; // 距离开始节点的最短路径距离
    }
}

边（GraphEdge）

1
2
3
4
5
6
7
8
class GraphEdge {
    // 边：skey -> tkey
    constructor(skey, tkey, weight) {
        this.skey = skey; // 边的开始节点
        this.tkey = tkey; // 边的结束节点
        this.weight = weight; // 边的权重
    }
}

图（Graph）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Graph {
    constructor() {
        this.nodes = {}; // 图中所有节点
    }
    /**
     * 新增一条边：skey -> tkey
     * @param {string} skey 开始节点标识
     * @param {string} tkey 结束节点标识
     * @param {number} w 边的权重
     */
    addEdge(skey, tkey, w) {
        this.nodes[skey].edges.push(new GraphEdge(skey, tkey, w));
    }
}

最小堆

这里的最小堆主要用于实现优先队列，它能在O(1) 时间内，快速得到当前距离源点最近的节点。

堆使用heap.js实现：

1
2
3
4
5
6
7
8
9
10
11
const { Heap } = require("heap-js");
class DistPriorityQueue {
    constructor() {
        this.minHeap = new Heap(this.heapComparator);
    }
    // 小顶堆，主要用于快速计算目前哪个未被访问的、距离开始节点最近的节点
    heapComparator(a, b) {
        return a.dist - b.dist;
    }
}

dijkstra算法实现

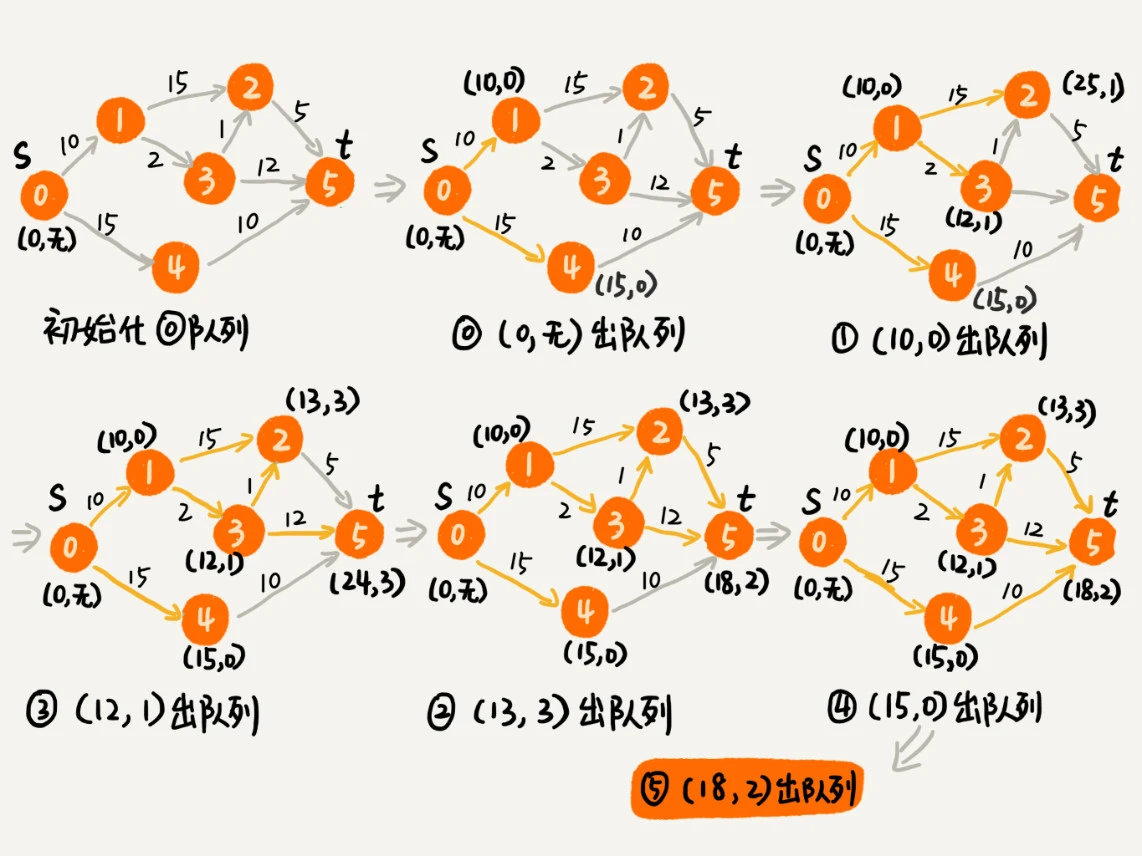
Untitled.png

实现思路

这里简单记录大体的思路，具体可见上图。

初始化所有的节点，除了开始节点本身dist设置为0，其他节点的dist均为最大值（方便之后比较）。同时将开始节点入优先队列。

从优先队列中取出距离开始节点最近的节点，检查此节点是否是目标节点，如果是，那么说明已经到达目的地，此时为最短距离，结束算法。

否则，开始尝试往下继续走，访问此节点的邻居节点：

  • 当前节点的dist +邻边长度 < 邻边节点的dist，那么说明从当前节点过来距离更短，更新邻边节点的dist值。

    如果队列中存在邻居节点，那么就更新update（其实就是更新节点的dist之后，对堆重新排序）；如果不存在，那么就将其放入队列中。

  • 当前节点的dist +邻边长度 ≥ 邻边节点的dist，那么说明这条路更长，没有必要走，不做任何处理。

一直持续，直到走到目的节点。

🌟🌟🌟优先队列的作用
能够快速拿到目前距离开始节点最近的节点（堆顶元素），从而每次都从最近的节点出发，一步步遍历到目的节点。

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/**
 * @param {Graph} graph 图
 * @param {string} skey 开始节点的标识
 * @param {string} tkey 结束节点的标识
 */
function dijkstra(graph, skey, tkey) {
    // step0: 用来保存最短路径，用于输出打印
    //      key和value代表路径方向，从value走到key：key <- value
    const pathNodes = {};

    // step1: 初始化每个节点距离开始节点的距离（dist属性）
    //      除了自己设置为0，其它都是最大值
    for (const key in graph.nodes) {
        const node = graph.nodes[key];
        node.dist = key === skey ? 0 : Number.MAX_VALUE;
    }

    // step2: 优先队列（小顶堆），用于取出dist属性最小的点，也就是距离开始节点最近的点
    const queue = new DistPriorityQueue();
    queue.minHeap.push(graph.nodes[skey]);

    // step3: 防止同一个节点，被多次添加到queue中（环），造成无限循环
    const visited = {};
    visited[skey] = true;

    // step4: 每次都取出未遍历到的，最近的点
    //        然后遍历最近的点的邻居节点
    //        如果邻居节点满足条件（具体看内循环），则增加到queue中
    while (queue.minHeap.size()) {
        // 每次拿到的都是距离开始节点最近的点
        // 最小堆可以保证在O(logN)内拿到
        const minDistNode = queue.minHeap.pop();
        // 到达目的地
        if (minDistNode.key === tkey) {
            break;
        }
        for (const edge of minDistNode.edges) {
            const linkedNode = graph.nodes[edge.tkey];
            // 当前距离开始节点最近的点，继续往邻居节点“走”
            // 如果距离+走的距离，比邻居节点到开始节点距离还小的话
            // 那么更新邻居节点的dist属性，更新pathNodes，并且更新queue
            if (minDistNode.dist + edge.weight < linkedNode.dist) {
                linkedNode.dist = minDistNode.dist + edge.weight;
                pathNodes[linkedNode.key] = minDistNode.key;

                if (visited[linkedNode.key]) {
                    queue.minHeap.remove(linkedNode);
                    queue.minHeap.push(linkedNode);
                } else {
                    queue.minHeap.push(linkedNode);
                    visited[linkedNode.key] = true;
                }
            }
        }
    }
    console.log(">>> 路径是", pathNodes);
}

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 测试代码
const a = new GraphNode("a");
const b = new GraphNode("b");
const c = new GraphNode("c");
const d = new GraphNode("d");
const e = new GraphNode("e");

const graph = new Graph();
graph.nodes = {
    a,
    b,
    c,
    d,
    e,
};
graph.addEdge("a", "b", 3);
graph.addEdge("a", "c", 1);
graph.addEdge("b", "e", 2);
graph.addEdge("c", "d", 1);
graph.addEdge("d", "e", 2);
// 输出：>>> 路径是 { b: 'a', c: 'a', d: 'c', e: 'd' }
// 逆序排列下就是路径顺序了：e <- d <- c <- a
dijkstra(graph, "a", "e");

实际地图项目-近似最短路径

实际工程应用中的取舍

对于实际地图，考虑全部的点和边固然可以得到最有解，但是计算复杂度高O(E*logV)

一般在实际工程中，只要取个近似解即可。

如何取近似解？

我们发现，最优路径一般在两个点之间的连线，不会向“外”绕。

分2种情况：

  • 两个点距离比较近（比如5公里），那么根据2个点做直线，并且点是直线中点。
    然后勾出一个矩形，根据规律只考虑矩形内的路径和点即可
  • 两个点距离比较远（比如500公里），那么按照方法1，也会有很多的路径和点。
    此时，只考虑国道、省道等主干道即可。
    类似高德地图，当地图缩小到一定比例，无关紧要的点和路径，都不再显示。当行驶过程中，动态加载计算附近的路径和点即可（详细地）。

这两种处理思路的主旨是忽略一些不重要的路径和点。

参考

极客时间-数据结构与算法之美