认识哈希链表
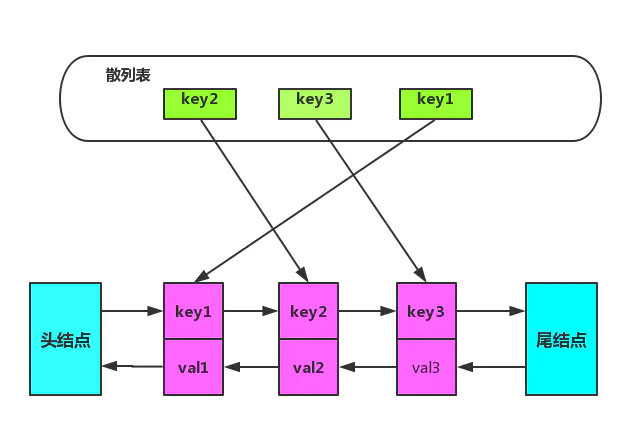
本质就是:散列表+链表。它被用于实现LRU等算法。
作用:
- 散列表:提供O(1) 复杂度下的快速读
- 双向链表:提供 O(1) 复杂度下的快速增删修改
认识LRU算法
LRU 是 Least Recently Used 的缩写,这种算法认为最近使用的数据是热门数据,下一次很大概率将会再次被使用。而最近很少被使用的数据,很大概率下一次不再用到。当缓存容量的满时候,优先淘汰最近很少使用的数据。
LRU 算法具体步骤:
- 新数据直接插入到链表头部
- 缓存数据被命中,将数据移动到链表头部
- 缓存已满的时候,移除链表尾部数据
LRU算法特点:
- 容量有上限,用于本地缓存能防止被撑爆。
- 缓存命令中率高。清空缓存时,先清空不经常被访问的缓存;如果缓存经常被访问,那么会一直保存
- 读写性能高,时间复杂度均为O(1)
利用LRU优化本地缓存
数据结构
基于LRU的哈希链表实现。
为什么选择哈希链表实现?
0、从需求出发,考虑使用哪些数据结构:要求快速访问,读O(1);快速增删,写O(1)
1、哈希链表 = 哈希表 + (双向)链表
2、链表:O(1) 时间内快速增删,但是读复杂度O(N)
3、哈希表:更次存入链表时,每个节点有2个字段,key和value;同时更新map。
下次需要查缓存时,直接根据key,从map中读取缓存值即可,复杂度是O(1)
在nodejs中,双向链表库使用了 yallist.js :
- 只支持插入尾部,不支持插入头部。所以和常见的lru的链表相反,尾部节点是最新命中节点,头部是最远命中节点
- yallist每个节点的结构是 { value, prev, next } 。prev保存上一个节点引用,next保存下一个节点引用。例如:想要访问其上的值,要访问:node.value.value
- 由于保存了prev和next指针,因此其上的removeNode等方法的复杂度是O(1),不需要像单链表那样从头到位遍历
代码
引入yallist,并且定义缓存节点类型:
1
2
3
4
5
6
7
8
9
| const yallist = require("yallist");
class Node {
constructor(key, value) {
this.key = key;
this.value = value;
}
}
|
实现LRU:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
class LRUCache {
constructor(capacity = 10) {
this.map = new Map();
this.doubleLinkedList = yallist.create([]);
this.capacity = capacity;
}
get(key) {
if (this.map.has(key)) {
const node = this.map.get(key);
this.put(key, node.value.value);
return node.value;
}
return null;
}
put(key, value) {
if (this.map.has(key)) {
this.doubleLinkedList.removeNode(this.map.get(key));
} else {
if (this.doubleLinkedList.length === this.capacity) {
const headNode = this.doubleLinkedList.head;
this.map.delete(headNode.value.key);
this.doubleLinkedList.removeNode(headNode);
}
}
this.doubleLinkedList.push(new Node(key, value));
this.map.set(key, this.doubleLinkedList.tail);
}
print() {
console.log("output1: ", this.map.keys());
console.log("output2: ", this.doubleLinkedList.toArray());
}
}
|
可以在leetcode上做题:
bookmark
